[Rancid]

The fuck kind of stupid shit are you talking about name_xox?

[Lexington]

Most 3D programmers or 3D computer Artist will use the 4 Dimensional Co-ordinate of W, X, Y, Z lines or points

The W used in 3D graphics is kind of an artifact of how projections and transformations are done. See here.

[Rancid]

The fourth dimension is added to make processing translations in addition to rotations easier. You can also use it for scaling.

That said, what does this have to do with the original premise of the thread?

[Lexington]

It has no clear relation, transformation, scaling, or rotation, to the original topic. No matrix, with no matter how many dimensions, can possibly relate it back. No yaw, pitch, or roll; no normal vector or vertex...we will never return to the original intent.

[One Degree]

Numbers definitely exist. Without them I would not know when it was time to buy more beer.

[Smertios]

Okay, I didn't watch the video because I got bored at the first few seconds. xD But I'll reply to this anyway.

First of all, this is one of the things I hate about philosophy: it asks the wrong questions. It obviously exists, otherwise we wouldn't be talking about it. The real question here is why they exist.

Would it be correct to say that a nominalist viewpoint would be that a number is "of something"... saying 1,748,392 means nothing, but saying 1,748,392 kg means something.

So, why is it that 1,748,392 kg means something. More specifically, what makes you conclude that 'kilograms' (and, thus, the whole concept of 'mass') exist, but not 'numbers'? Many people will be tempted to say that mass obviously exists because you can feel it. But can you? After all, how do we define mass? m = F/a is a good starting point. And that pretty much one of the ways how you would measure mass. You apply a force to an object, and measure its acceleration. So, does mass really exist, or is it just a part of the of force/acceleration relationship, like 1,748,392 is simply part of the mass of the object you invented there.

In the end of the day, numbers are just a mathematical abstraction we use to simplify our lives. Just like mass is a physical abstraction that exists only because it is useful for us. The same can be applied to pretty much any science. For example, do genes exist? Genes are just a combination of letters (AAGTGCGTAGCT...), after all, or from a physical point of view, they are just a bunch of nucleotides that work together to synthesize proteins. But 'genes', as a concept, exist, because we have defined that concept as an abstraction to study how they work. Another example: does memory or ideas exist? They are just neurons interacting with one another, after all.

Similarly, pi (or tau if you prefer) is only a thing when it is applied to a circle. Without the circle, it isn't anything.

Why does a circle exist, then? It's a mathematical structure just like a number is. You can describe a circle using just numbers. In fact, just one number: either it's radius or its circumference.

I can certainly say that there are zero bananas on my desk, and I can understand a negative number in a more abstract way... I can't say there are -1 bananas on my desk (don't ask me why I'm fixated on bananas), but I can comprehend there being one less banana on my desk than could potentially be there. I usually just think of such things on a graph.

If you change 'bananas' and 'desk' to 'dollars' and 'bank', it starts making sense, though. If you have -3000 dollars in your bank account, that means you owe the bank money. It is, as a concept, as real as having 3000 dollars there.

I also don't have a problem with sqrt(-1) or other imaginary numbers, since I take the operative word "imaginary" literally. Maybe fictionalism makes more sense there, since it literally doesn't fucking exist ever anywhere, and that may work for more abstract concepts.

That's actually the worse approach you can take to imaginary numbers. xD They are about as real as any other number set. You can actually "feel" them just like you would "feel" natural numbers by counting something — let's say bananas on your desk. Just take two different phases from your electric panel and measure the voltage accross them. If either phase is 127 Volts, you'll sum those voltages and get... 220 Volts. Weird, no? Well, no, because AC voltage is a complex quantity. The 127 there refers just to its absolute value. The voltages in those phases are actually 127∠0° and 127∠120° (a complex number can be defined by polar coordinates as having a magnitude and an angle, but if you prefer cartesian coordinates, 127∠120° = -63.5 + 110*i).

Complex numbers are real and useful. They are not just mathematical structures that people invented for fun.

Dividing by zero I can imagine since I picture it on a graph



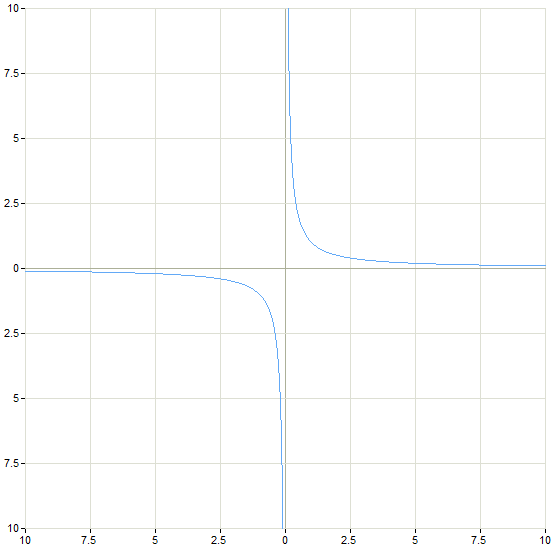
I'm not sure if that is technically nominalism or platonism or fictionalism though.

That's actually a tough one, as you need hyperreal numbers to define 1/0 = ∞ an 1/∞ = 0. But well, those are incredibly useful in calculus too.

But I don't think that "1" exists. "1" is specifically 1 of something. You don't have to necessarily mention or define that something, but 1 unit divided by 2 units is half of 1 unit.

Thoughts?

Yes, in "1 unit of stuff", '1' exists just as much as 'unit' or 'stuff'. If you take physical units, for example, you'll see that they all have circular definitions: http://en.wikipedia.org/wiki/SI_base_unit#The_seven_SI_base_units. The definition of meter depends on the velocity of light, which depends on the definition of second, which depends on the definition of kelvin, which depends on the definition of mole, which depends on the definition of kilogram, which depends on the definition of meter (the international kg prototype has defined proportions after all). So how can we say that any of those units/quantities actually exist? They are just abstractions we use to represent phenomena (like meters being used to determine how much light can travel in I-don't-know-how-many-seconds), just like numbers are abstractions we use to represent phenomena (like how many bananas are on your desk right now).

[Smertios]

An imaginary number is a means to help deal with transitions (or rotations) between positive and negative sides of the number line. We're just adding a dimension to the number line. I'm not so sure that imaginary really mess with other math concepts. The hell would I know though. It sure as hell makes sense to me from an engineering sense.

I have been thinking a lot about this lately, and I think this approach to complex numbers is not the most didactic one. Don't get me wrong, you are 100% correct in all your assertions. I just think that explaining how i = srqt(-1) is a better alternative.

While it is true that from going to R to C, you are adding one dimension, and from going back from C to R, you are subtracting one dimension; that is counter-intuitive to someone who is learning about number systems. And that's mainly because it gives the false impression that, to go from one set to the other, all you need to do is add or subtract dimensions, and that you can add and subtract dimensions freely.

You can't do that.

In the sequence N - Z - Q - R - C - H - O, the only situation in which you are adding/subtracting a dimension is when you go from R to C (and vice-versa). When you go from R to Q, you are not subtracting a dimension (the rationals don't have 0 dimensions. Similarly, Hamilton showed that you can't have a number with 3 dimensions. The next step after the complex numbers are quaternions, which have 4 dimensions — e.g., (4 + 2i + 7j + 2k) ∈ H.

Also, it's important to notice that C is different from R². In R², you have points formed by a pair of coordinates (x,y) = xî + yĵ, and x and y, or between î and ĵ. In C, you have a number (a,b) = a + bi formed by two coordinates a and b. But there is a clear relationship between i and 1. That is, i² = 1.

[Rancid]

Smertios, you hurt by brain.

Here's what I'll follow that up with.

I work on video compression, and we LOOOOOVE to use the discrete cosine transform (DCT), rather than the DFT because a DCT produces all real numbers. Therefore, to tell with imaginary numbers! They are the work of Satan himself.

[lucky]

I have been thinking a lot about this lately, and I think this approach to complex numbers is not the most didactic one. Don't get me wrong, you are 100% correct in all your assertions. I just think that explaining how i = srqt(-1) is a better alternative.

That's the historical way mathematicians operated, before the logical basis was fully worked out. As a result, nobody was completely sure whether what they were doing was making any sense or not. Some results (e.g. by Euler) were indeed incorrect because of that. The name "imaginary numbers" was a result of that historical lack of confidence, and unfortunately it stuck, forever causing confusion to students.

I much prefer the modern treatment, with proper definitions.

Somebody saying "imagine sqrt(-1) exists even though you already know it doesn't" would just cause a protest and a rejection of the whole idea as bogus from my younger self.

Kind of how I rejected "pretend an infinitely small real number dx exists, even though we all know it doesn't" as dumb when my high school physics teacher tried to do calculus that way. It wasn't until college that I really appreciated the beauty of mathematical analysis because until then it was tainted to me with nonsense notation like that, so I was repelled from the whole subject. Even though I did already know proper definitions of derivatives and such. It is unfortunate that people still teach calculus like that. The whole "dy/dx" notation should be expelled from school books because it only causes a lot of confusion about what it really means.

It's stuff like that that gives math a bad name in schools. It seems strange and mystical because it's taught as if it was about believing and memorizing weird stuff because the teacher says so.

Again, professional mathematicians, such as Newton and Leibniz, actually did calculus that way in the old days, before logic, understandably causing a lot of doubt and controversy. Physicists actually still routinely do that. They need to catch up with modern math developments!

[AuRomin]

I would say that a number is like a color. I know that if I mix blue and red I get purple, so it can exist in my mind as an abstract, but it really is only practically used to describe objects, just as numbers are. Just imagine math problems as how colors mix. It is fun.

The only way that we can conceive of numbers is by external experience. We learn one by seeing one of something and learning to identify the modifier. When working with complex numbers we are just working with abstract modifiers. The real question is, is it useful to do this? If not, this whole thing is meaningless.

[Saeko]

I have been thinking a lot about this lately, and I think this approach to complex numbers is not the most didactic one. Don't get me wrong, you are 100% correct in all your assertions. I just think that explaining how i = srqt(-1) is a better alternative.

While it is true that from going to R to C, you are adding one dimension, and from going back from C to R, you are subtracting one dimension; that is counter-intuitive to someone who is learning about number systems. And that's mainly because it gives the false impression that, to go from one set to the other, all you need to do is add or subtract dimensions, and that you can add and subtract dimensions freely.

You can't do that.

In the sequence N - Z - Q - R - C - H - O, the only situation in which you are adding/subtracting a dimension is when you go from R to C (and vice-versa). When you go from R to Q, you are not subtracting a dimension (the rationals don't have 0 dimensions. Similarly, Hamilton showed that you can't have a number with 3 dimensions. The next step after the complex numbers are quaternions, which have 4 dimensions — e.g., (4 + 2i + 7j + 2k) ∈ H.

Also, it's important to notice that C is different from R². In R², you have points formed by a pair of coordinates (x,y) = xî + yĵ, and x and y, or between î and ĵ. In C, you have a number (a,b) = a + bi formed by two coordinates a and b. But there is a clear relationship between i and 1. That is, i² = 1.

I don't think that the N - Z - Q - R - C approach is good at all, despite the fact that that was how I was taught. This constructionist approach is based on set theory and is motivated mainly by the need for (overly) formal proofs. This approach requires a number of arbitrary definitions which are virtually impossible to justify on intuitive grounds.

The best pedagogy, in my opinion, is the historical one. That is, start with geometry, and introduce the positive natural and then rational numbers from the get go. After that, you motivate irrational numbers with the pythagorean theorem and a proof of the irrationality of the square root of two. Then, with cartesian geometry, introduce the negative numbers. Next, using equation solving introduce the imaginary numbers. Finally, in calculus, the student should be exposed to the continuum axiom and the entirety of the real and complex numbers.

[Harmattan]

Numbers simply quantify proportionality.
A length of 1.7 meters is simply a length 1.7 times longer than a 1 meter length. This is really as simple as that: physically speaking, numbers are always proportions. And proportionality has an indisputable physical existence.


Complex numbers have no physical existence, they are calculus artifacts.
In physics the imaginary part is of no interest in the end result! Never. Hence why "imaginary" is a very fitting name: it has no physical importance.

For example a sinusoidal wave is often represented by a complex function. But this is an abusive shortcut. Actually those waves are represented by real functions such as phi(t) = a.cos(wt + b). But working with trigonometric functions is tedious so we simply remark that phi(t) = Re(a.e ^(i(wt +b))). A simple trick. Abusively we omit the "Re" function. Nevertheless, only the real part of the complex functions represents the wave, the imaginary part s simply associated for convenience purpose.

I much prefer the modern treatment, with proper definitions.

Somebody saying "imagine sqrt(-1) exists even though you already know it doesn't" would just cause a protest and a rejection of the whole idea as bogus from my younger self.

Kind of how I rejected "pretend an infinitely small real number dx exists, even though we all know it doesn't" as dumb when my high school physics teacher tried to do calculus that way. It wasn't until college that I really appreciated the beauty of mathematical analysis because until then it was tainted to me with nonsense notation like that, so I was repelled from the whole subject. Even though I did already know proper definitions of derivatives and such. It is unfortunate that people still teach calculus like that. The whole "dy/dx" notation should be expelled from school books because it only causes a lot of confusion about what it really means.

Complex numbers puzzle people because they are not told that they are mere calculus tricks.

Whether one introduces an algebraic set with specific operators, or a constant worth sqrt(-1), the problem remains: people do not understand why nature requires this. Once you clarify that complex numbers are mere tricks, then it is easier to present mathematical situations where complex numbers can help. And in those cases it seems natural to introduce a constant i such as i² = -1. This is not the case with an algebraic introduction: you start from the solution rather than the problem.

In my opinion presenting an algebraic formalization is nice for students already familiar with complex numbers and algebra. But introducing them right off the bat this way seems harmful. This is as much puzzling, this is harder to memorize, and you add another puzzling question: why do I need elements from the complex set in an equation that was only defined with real elements in order to determine a real solution? And as I already said, the algebraic definitions are not naturally introduced from the problem to solve.


As for the dx/dt notation, it is perfectly fine for physics. If I increment the time by dt, how does the position evolves? This is what derivatives answer. This is naturally connected with the tangent slope interpretation. And I do not see what else you would like to use instead for multivariate functions.

[lucky]

Hence why "imaginary" is a very fitting name: it has no physical importance.

Actually, complex numbers are central to quantum mechanics. The Schrödinger's equation is a differential equation over complex functions, there is a factor of i in it.

You could say it's "just a notational convenience", and it's true, but it's also true of every other mathematical object that people have ever defined. Convenience is the whole reason for definitions in mathematics.

And I do not see what else you would like to use instead for multivariate functions.

One common notation for the derivative with respect to x is: "D_x f". Another common notation is f'_x. Any notation will do as long as it doesn't involve manipulating objects that have not been defined before.

I'd be more accepting of the df/dx notation if everybody was clear that it's just a funny notation and not an actual ratio of two objects. Unfortunately, they aren't. For instance, they start writing shit like df = x dx. This immediately leads to errors, for instance, it's not true that df/dt = df/dx * dx/dt when f is a function of two variables x and y, which are both in turn a function of t. Thoroughly confusing and unnecessary nonsense.

[Rancid]

In physics the imaginary part is of no interest in the end result! Never. Hence why "imaginary" is a very fitting name: it has no physical importance.

In signal processing, the imaginary component of say an IIR filter is very important and most certainly has physical importance.....

Or rather, if it weren't important or needed, we wouldn't use it.

[Harmattan]

Actually, complex numbers are central to quantum mechanics. The Schrödinger's equation is a differential equation over complex functions, there is a factor of i in it.

And it could be rewritten to not use complex numbers. For example the Schrodinger equation could be split into two real equations a wave function should obey.

Real numbers are physical observables: they quantify proportionality. Complex numbers are not observables. At best you can observe their magnitude and phase, two independent real properties that could be used to describe a real wave or a complex wave.

I'd be more accepting of the df/dx notation if everybody was clear that it's just a funny notation and not an actual ratio of two objects. Unfortunately, they aren't. For instance, they start writing shit like df = x dx. This immediately leads to errors, for instance, it's not true that df/dt = df/dx * dx/dt when f is a function of two variables x and y, which are both in turn a function of t. Thoroughly confusing and unnecessary nonsense.

But those are ratios and what you did is actually legit. And if you choose dx such as dx = x(t + dt) - x(t), as one should expect, then the result is what is naively expected.

Ex: let f(t) = ln(t)^2 and x(t) = ln(t)
Then: df/dt = df/dx * dx / dt

In signal processing, the imaginary component of say an IIR filter is very important and most certainly has physical importance.....

No, it is important for your mathematical model of reality. Not for reality itself. One could build another model that does not use complex numbers.

[lucky]

And it could be rewritten to not use complex numbers. For example the Schrodinger equation could be split into two real equations a wave function should obey.

Ha. Of course. Instead of complex numbers, we could be using pairs of real numbers. We could even define some nice operations operating on these pairs of real numbers together, such as addition and multiplication, so that we don't have to duplicate notation separately for each coordinate. And then we'd like a name for these pairs-of-real-numbers-with-interesting-operations-that-make-them-a-field objects, so that we don't have to repeat the definition of the operations every time. Maybe we could name them... I don't know... "complicated numbers" or something like that?

But those are ratios and what you did is actually legit.

You misread what I wrote, so I'll give an example.
f = x * y
df/dx = y, df/dy = x
x = 5t
dx/dt = 5
y = 6t
dy/dt = 6
At t=2 we have: x=10, y=12, df/dx = y = 12.
So if you're a confused student who thinks these dx's are kind of like regular little real numbers, you'll get:
df/dt = df/dx * dx/dt = 12 * 5 = 60
when in fact:
df/dt=120 at t=2.

Besides: even if you were getting the right answers by doing this, it's still pointless. Define what you mean by "dt" before you start talking of ratios.

Maybe they tell you: in a case like the above, remember to do something different, and then it works fine. How do you *know* for sure whether you're getting the right answer or not by doing such manipulations on things that nobody has even bothered to define for you (like the magical "dt" here)? How do you know you get a valid equation when you move a dx from one side of an equation to another? Because your math teacher said it's OK? It's extremely anti-educational to tell a student to start doing things on trust. Especially when teaching mathematics, because mathematics is the exact opposite of trusting an authority. The whole reason for doing mathematics is to derive precise proofs from precise definitions, not to just carry out some algorithms that somebody else told you to carry out and to hope it all works out fine. Otherwise it becomes an incomprehensible and meaningless subject, like it actually does for most students.

[Harmattan]

Ha. Of course. Instead of complex numbers, we could be using pairs of real numbers.

No. Instead of a complex wave you could use a single real wave. But it should obey two equations instead of one.

when in fact:
df/dt=120 at t=2.

Ok, the problem is different from what you have stated but I get your point: there are students who think that f'(t = 2) can be computed by doing (f(2) - f(0)) / (2 - 0).

That being said I am not convinced the problem is that big nor that changing the notation would fix it as you would still have to teach them the tangent slope interpretation and the analytical computation through a limit to zero.

Besides: even if you were getting the right answers by doing this, it's still pointless. Define what you mean by "dt" before you start talking of ratios.

I really fail to see why there would be a problem to define dt, why it would involve trust into authority or magical rules. It is just a fucking division and as long as it is not zero I can freely move it from one side of the equation to the other, just like for any regular division.

The only rule is that df/dt is the derivative only if df means f(t + dt) - f(t) and dt is infinitesimal.

[lucky]

Instead of a complex wave you could use a single real wave. But it should obey two equations instead of one.

Show me.

Ok, the problem is different from what you have stated but I get your point: there are students who think that f'(t = 2) can be computed by doing (f(2) - f(0)) / (2 - 0).

That was not my example at all, but I'll just let it go.

I really fail to see why there would be a problem to define dt, why it would involve trust into authority or magical rules. It is just a fucking division [...] dt is infinitesimal.

So you're saying dt is a real number and dt is infinitesimal? Define infinitesimal.

[Harmattan]

Show me.

No, this would take far too long and it may even be practically very difficult. However there is no theoretical obstacle to such a reformulation.

So you're saying dt is a real number and dt is infinitesimal? Define infinitesimal.

The invert of infinite. This is not more troublesome than the concept of infinite, which is needed for most of mathematics.

[lucky]

The invert of infinite.

OK. Infinity is indeed a useful concept, but it's not a member of the set of real numbers. Sometimes people define the set of "extended real numbers", i.e. R* = R + {-infinity, +infinity}. In that case, 1/infinity = 0, by definition. But clearly that doesn't work for your purposes, because you said it's non-zero. So you need an alternative definition. I haven't seen one that would result in a different real number. So you'd have to be specific.

Notice that R* is ironically also a counter-example to your claim that real numbers are all there is, because it contains things that are not real numbers.

Anyway, you're in the weeds, so I'll stop you right here before you get any deeper. There are obviously no "infinitesimal real numbers". For instance, there is no positive real number x such that x < 1/n for all positive integers n. That's easily proven. So your further attempts at such a definition are bound to fail. You're welcome to try.

Interestingly, it's possible to create a number system with infinitesimals, but that would not be the real numbers. One such construction is called "hyperreal numbers". But that only weakens your claim that real numbers are all there is, so you probably don't want to go there.